Well, I got carried away with the difference games, eh?

Constructing the thermograph
Truth to say, difference games are not necessary to thermography at all, and are hardly ever used. However, it was easy to show that the keima sente and the crawl sente are unnecessary. The kosumi sente dominates them. As I said, if they were gote, that would be a different matter. But anyway, all we have to consider are the kosumi sente and the large monkey jump sente. Let's review the reverse sente first.
- Click Here To Show Diagram Code
[go]$$Wc Reverse sente, Black continues
$$ -----------------
$$ | C 4 2 3 C C O |
$$ | X X 1 C C C O |
$$ | . X O O O O O |
$$ | . X X X O O C |
$$ | . . . X O O O |
$$ | . . . X X X X |
$$ | . . . . . . . |
$$ -----------------[/go]

blocks on the second line. Play can, and usually does, stop there. If Black replies she plays the hane-and-connect for a local score of -5 in the marked region. Each player has made the same number of plays, so the Right wall of the thermograph rises as a vertical line at that point.
Black does not reply above temperature 1, so the wall turns 45° to the left at that temperature rising one degree for each point of territory. Remember, the leftward movement is positive, the reverse the usual convention. The equation of that line is
v = -6 + t, where
v is the territory and
t is the temperature.
Now let's look at the kosumi sente.
- Click Here To Show Diagram Code
[go]$$Bc Kosumi sente, Black continues
$$ -----------------
$$ | . . 1 3 4 . O |
$$ | X X 5 2 . . O |
$$ | . X O O O O O |
$$ | . X X X O O . |
$$ | . . . X O O O |
$$ | . . . X X X X |
$$ | . . . . . . . |
$$ -----------------[/go]
The sente actually ends with

but we consider what happens when Black keeps playing. The score after
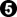
is -2. Black has made one more move than White, so the line from here angles up and to the right. It's equation is
v = -2 - t. How far up does it go?
- Click Here To Show Diagram Code
[go]$$Wc Kosumi sente, White follow-up
$$ -----------------
$$ | . . B 1 . . O |
$$ | X X 2 W . . O |
$$ | . X O O O O O |
$$ | . X X X O O . |
$$ | . . . X O O O |
$$ | . . . X X X X |
$$ | . . . . . . . |
$$ -----------------[/go]
If I didn't already know, it would be easy to work out that this is correct play at temperature 1. White could get an equivalent result, except for ko threats, by starting at
2. Each player has made the same number of plays, including the kosumi sente exchange, so the line rises vertically at -3. These two lines intersect at v = -3, t = 1. Above temperature 1 the prospective wall, called a
scaffold, rises vertically at -3, below temperature 1 it angles down to -2 at temperature 0.
Now let's look at the monkey jump.
- Click Here To Show Diagram Code
[go]$$Bc Monkey jump sente 1
$$ -----------------
$$ | . . 3 4 1 . O |
$$ | X X 2 5 6 . O |
$$ | . X O O O O O |
$$ | . X X X O O . |
$$ | . . . X O O O |
$$ | . . . X X X X |
$$ | . . . . . . . |
$$ -----------------[/go]
This is one of the main lines, with the throw-in,
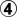
. White could also get here by starting at
4. That's the other main line. The usual reply is at
6. We'll consider that later.
What if Black continues?
- Click Here To Show Diagram Code
[go]$$Bc Monkey jump sente 1, Black continues
$$ -----------------
$$ | . 9 B 7 B 8 O |
$$ | X X W B W . O |
$$ | . X O O O O O |
$$ | . X X X O O . |
$$ | . . . X O O O |
$$ | . . . X X X X |
$$ | . . . . . . . |
$$ -----------------[/go]
1

prisoner
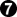
connects the Black stones,

makes a second eye, and

saves the four stones. The local score is 0. Since Black has made one more move than White, the scaffold angles up from 0 to the right at one point of territory for each degree of temperature. The equation of the line is
v = -t.
How high does it go? To find out, let's look at the White follow-up after the sente.
- Click Here To Show Diagram Code
[go]$$Wc Monkey jump sente 1, White follow-up.
$$ -----------------
$$ | . 2 B 3 B 1 O |
$$ | X X W B W . O |
$$ | . X O O O O O |
$$ | . X X X O O . |
$$ | . . . X O O O |
$$ | . . . X X X X |
$$ | . . . . . . . |
$$ -----------------[/go]
1

prisoner
There is a ko, which White can take and win on the usual assumption of no ko threats. But

comes to the same thing.

After

the local score is -4. Since White has made one more move than Black, the scaffold angles up from there to the left. It's equation is
v = -4 + t. Note that this is the scaffold for the position after the sente, not the scaffold for the original position. The scaffolds intersect at t = 2, v = -2. The mast rises vertically from there. The scaffold for this sente is v = -2 above temperature 2 and v = -4 + t below temperature 2.
There is another variation to consider.
- Click Here To Show Diagram Code
[go]$$Bc Monkey jump sente 1a
$$ -----------------
$$ | . . 3 5 1 6 O |
$$ | X X 2 . 4 . O |
$$ | . X O O O O O |
$$ | . X X X O O . |
$$ | . . . X O O O |
$$ | . . . X X X X |
$$ | . . . . . . . |
$$ -----------------[/go]
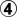
does not play the throw-in, but it threatens it.
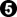
prevents that, with sente. As we have seen, with a different order of play, this line is incomparable with the throw-in. After

the local score is -1. The scaffold rises vertically from there. OC, that is worse for White than -2, so this line is not as good as the throw-in
above temperature 2. But it is better for White than 0, so we find the intersection
v = -t and
v = -1 to find where White switches to this line of play. The intersection is at t = 1, v = -1. So for the reply of

the scaffold is vertical at -2 above temperature 2, angling down below temperature 2 to -1 at temperature 1, and vertical below that to -1 at temperature 0.

BTW, what if Black does not connect with
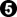
in the previous diagram, but tries to kill?
- Click Here To Show Diagram Code
[go]$$Bcm5 Monkey jump sente 1a, variation
$$ -----------------
$$ | . . B 2 B 1 O |
$$ | X X W 3 W a O |
$$ | . X O O O O O |
$$ | . X X X O O . |
$$ | . . . X O O O |
$$ | . . . X X X X |
$$ | . . . . . . . |
$$ -----------------[/go]
Now White cannot play at
a because of damezumari. Oh, for a dame!
- Click Here To Show Diagram Code
[go]$$Wcm8 Monkey jump sente 1a, variation
$$ -----------------
$$ | 2 1 B 3 B B O |
$$ | X X W B W 5 O |
$$ | . X O O O O O |
$$ | . X X X O O . |
$$ | . . . X O O O |
$$ | . . . X X X X |
$$ | . . . . . . . |
$$ -----------------[/go]
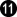
at
8White has no external threats, by assumption, but the play has generated a local threat for White at

. With a dame White would not have needed to play the ko.

More later.



