RobertJasiek wrote: Bill Spight wrote: Assuming that this is Black's threat, there is a swing of 31 pts. in 5 moves, for an average gain of 6.2 pts. per move. However,  actually makes a larger ko by giving up an extra stone when White wins the ko, for a swing of 32 pts. in 5 moves, or an average gain of 6.4 pts. per move. That makes  sente, so White will take and win the resulting larger ko. Why do you speak of "sente"? What is "sente" in a tree of a local ko endgame? Just an informal word to express that a player's local play is correctly answered by the opponent's next move being a local play?
You may consider "sente" to be informal here, but in the context of kos the term can acquire new technical meanings, if one bothers to define them. In this case, raising the temperature is part of the meaning. Because White is komaster, we already know that White's answer is correct play.
RobertJasiek wrote: We can calculate the average gain of either variation because there is only one sequence started by White. In other initial positions, can it happen that there would be two or more sequences started by White to be considered? If yes, how to calculate each average gain, compare and decide between variations?
You are asking a lot! 
As is well established, non-ko positions may be solved (in the sense of finding their mean values and temperatures) by using the method of multiples to find mean values (counts), from which miai values (temperatures) may be derived. They may also be solved using thermography. You can even apply the method of multiples to placid ko positions. But hyperactive kos require thermographic ideas to solve. That is, correct local play depends crucially upon the environment in a way that the method of multiples does not address. For one thing, with hyperactive kos we do not speak of mean values, but of mast values. The mast, OC, is a thermographic concept.
The approach which I have taken here is top down, to attempt to find the temperature (average gain per play) above which at least one player will prefer to play elsewhere (assuming an ideal environment). If the position is too complicated to do that and proceed top down, the task becomes more difficult and laborious.
RobertJasiek wrote: Why do you speak of "threat"? Is it not easier to speak of choice, strategy or tactical variation?
I speak of Black's threat because we do not expect Black, as koloser, to be able to carry it out. But we need to know it because we need to know when it is too small for White to prevent it. Assuming that we have found White's correct play and Black's correct threat, when the average gain of plays elsewhere (in the environment) is equal to the average gain of the ko plays, White will be indifferent between preventing Black's threat or not.
The concept of threat helps to explain the discussion below. 
RobertJasiek wrote: Quote: However,  actually makes a larger ko by giving up an extra stone when White wins the ko, for a swing of 32 pts. in 5 moves Let me try to understand how to calculate the tally and after what sequences' followers to calculate the swing:
- Click Here To Show Diagram Code
[go]$$B initial sequence
$$ ---------------------------
$$ . X X . . X 4 1 O . . O O .
$$ . X . O O . X O 3 X X . O .
$$ . X . O O . X O . X X . O .
$$ . X X X X X X O O O O O O .
$$ . . . . . . . . . . . . . .[/go]
If you want to calculate the swing you have to let Black finish her threat.
Quote: Initial prisoner difference = 0. Initial excess plays = 1.
- Click Here To Show Diagram Code
[go]$$B Black continues
$$ ---------------------------
$$ . X X . . X O 5 O 7 . O O .
$$ . X . O O . X O X X X . O .
$$ . X . O O . X O . X X . O .
$$ . X X X X X X O O O O O O .
$$ . . . . . . . . . . . . . .[/go]
There is potential for confusion here. As koloser, Black should not be able to take the ko back.
But you did finally let Black complete her threat. 
Quote: Black continuation's excess plays = 2. Black follower's count including the initial prisoner difference = 16 + 0 = 16.
- Click Here To Show Diagram Code
[go]$$B White continues
$$ ---------------------------
$$ . X X . 8 X O . O . . O O .
$$ . X . O O 6 X O X X X . O .
$$ . X . O O . X O . X X . O .
$$ . X X X X X X O O O O O O .
$$ . . . . . . . . . . . . . .[/go]
Black did not take back with 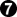 . Good. . Good. 
Quote: White continuation's excess plays = 2.
White follower's count including the initial prisoner difference = -16 + 0 = -16.
Total excess plays = initial excess plays + Black continuation's excess plays + White continuation's excess plays = 1 + 2 + 2 = 5.
Swing = 16 + (-16) = 32.
Is this calculation right?
Yes.
Quote: If yes, why does White being the komaster allow Black 5 in Black's continuation?
To discover Black's threat.
But, technically, having taken the ko with 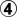 , as komaster White should not allow Black to take the ko back. , as komaster White should not allow Black to take the ko back.
RobertJasiek wrote: Quote:
- Click Here To Show Diagram Code
[go]$$B Black first
$$ ---------------------------
$$ . X X . 8 X W 1 O . . O O .
$$ . X . O O 6 X O 3 X X . O .
$$ . X . O O . X O . X X . O .
$$ . X X X X X X O O O O O O .
$$ . . . . . . . . . . . . . .[/go]
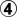 @  If Black cuts with  White can take the ko back, make a larger ko and win it for a score of -16 pts. in one net play, instead of getting a score -15 pts. in two net plays. It isn't just that  loses one point, it loses one play, as well.  is a mistake. I understand this but... a) Black starts this sequence. Why may we compare it to the sequence started by White to assess that the former has the mistake Black 3?
Because the comparison shows that  is worse than a pass. is worse than a pass.
RobertJasiek wrote: b) If we use this reasoning in your text to identify the mistake Black 3, why do we need the following cited analysis? Quote:
- Click Here To Show Diagram Code
[go]$$B Black first
$$ ---------------------------
$$ . X X . . X O 1 O 5 . O O .
$$ . X . O O . X O 3 X X . O .
$$ . X . O O . X O . X X . O .
$$ . X X X X X X O O O O O O .
$$ . . . . . . . . . . . . . .[/go]
In three moves Black can take the ko, make the larger ko, and win it. OC, White will prevent this from happening, but this is one threat. The resulting local score is 16 pts. (for Black). Assuming that this is Black's threat, there is a swing of 31 pts. in 5 moves, for an average gain of 6.2 pts. per move. However,  actually makes a larger ko by giving up an extra stone when White wins the ko, for a swing of 32 pts. in 5 moves, or an average gain of 6.4 pts. per move. That makes  sente, so White will take and win the resulting larger ko.
We do not actually need it. However, since we are working top down and trying to find Black's best threat, we initially allow  and and 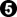 . Having done so, this line of reasoning enables us to discover that . Having done so, this line of reasoning enables us to discover that  is a mistake. is a mistake.
RobertJasiek wrote: Other topic: Quote:
- Click Here To Show Diagram Code
[go]$$B Black first
$$ ---------------------------
$$ . X X . . X W 1 O . . O O .
$$ . X . O O . X O 4 X X . O .
$$ . X . O O . X O . X X . O .
$$ . X X X X X X O O O O O O .
$$ . . . . . . . . . . . . . .[/go]
 @  Although White is the komaster, White 2 may not recapture due to the ko rule. White need not play 2 at 4 because he is the komaster and can force Black to first play at 3. Therefore, White's correct local move 2 is a pass.
I believe this comes from my analysis.  plays elsewhere because we want to discover Black's threat. Otherwise he would play his sufficiently large threat and take the ko back. plays elsewhere because we want to discover Black's threat. Otherwise he would play his sufficiently large threat and take the ko back.
RobertJasiek wrote: However, if White plays 2 at 4, Black's correct play in view of White being the komaster is to connect the ko. The resulting count is the same. IOW, the diagram shows a dominating White 2.
If  is at 4, the local temperature has dropped and Black should pass. is at 4, the local temperature has dropped and Black should pass.
RobertJasiek wrote: ***
Now, we might also analyse the case "neither player is komaster".
***
If neither player is komaster, whoever wins the ko fight must ignore a ko threat to do so. That means that the properties of ko threats become significant. There is no single way to handle the no komaster case for non-placid kos.
RobertJasiek wrote: While I am approaching an understanding of analysis of this example, the general method remains a mystery for me.
That's because you have not learned thermography. The theory of non-placid kos depends upon thermographic ideas.
RobertJasiek wrote: On Sensei's and here, you define active ko. I understand that it is rare. Uh. So rare that you do not know any example, can you show some or is it top secret?
Oh, it's not top secret, it's just not very important, and it is not so easy to explain. However, I should dig into my files and unearth an example or two.  Maybe I put up an example on rec.games.go many years ago. Maybe I put up an example on rec.games.go many years ago.
|
 and win it. (Probably not right away, OC, but we can skip the ko fight.) The result is a local score of -15 (15 pts. for White).
and win it. (Probably not right away, OC, but we can skip the ko fight.) The result is a local score of -15 (15 pts. for White). actually makes a larger ko by giving up an extra stone when White wins the ko, for a swing of 32 pts. in 4 moves, or an average gain of 8 pts. per move. (Edited for correctness after Robert pointed out that I miscounted the net number of moves.)
actually makes a larger ko by giving up an extra stone when White wins the ko, for a swing of 32 pts. in 4 moves, or an average gain of 8 pts. per move. (Edited for correctness after Robert pointed out that I miscounted the net number of moves.) @
@ 
 , leaving a small ko. Let's analyze it, with White komaster.
, leaving a small ko. Let's analyze it, with White komaster. is 0, with a local temperature of 1 pt. By comparison Black's threat to take and connect the ko with sente reaches a local score of 2 pts., and is the better threat. This result may seem counterintuitive.
is 0, with a local temperature of 1 pt. By comparison Black's threat to take and connect the ko with sente reaches a local score of 2 pts., and is the better threat. This result may seem counterintuitive. . Good.
. Good.  . Having done so, this line of reasoning enables us to discover that
. Having done so, this line of reasoning enables us to discover that  plays elsewhere because we want to discover Black's threat. Otherwise he would play his sufficiently large threat and take the ko back.
plays elsewhere because we want to discover Black's threat. Otherwise he would play his sufficiently large threat and take the ko back.