I've taken a small break from studying for the last few weeks. Now that I'm back, I have a couple of new study ideas.
For a while I've been aiming for a rather peaceful style. However, I'd like to try playing more fighting games now. I'm hoping this will expose more mistakes that I can learn from. For example, in a very peaceful game my opponent and I might only play about 60 points' worth of mistakes each. Even so I am still only about KGS 2 dan. I imagine that to reach KGS 5 dan I should be able to correct about 39 points (i.e. three handicap stones) of those mistakes. But out of 60 points of mistakes, it is sometimes quite difficult to find 39 points of mistakes that I can effectively study and fix. In a fighting game, at my level, it's not strange to see 150 points or more of mistakes from each side, and many more of these mistakes seem fixable.
My second thought is that I'd like to try reviewing some games from stronger players, e.g. pro or AI games, in addition to my own games.
Here's one such game. KataGo has a (new, I think?) "playout doubling advantage" configuration option which causes it to assume it is stronger than its opponent and play more tricky moves. This is a game between two KataGo instances that both assume their opponent is weaker. Also, black thinks the komi is 13 and white thinks it is 0. So they were both quite aggressive.
Game 28, position 1
- Click Here To Show Diagram Code
[go]$$Bc Pretty normal beginning
$$ ---------------------------------------
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . 2 . . . . . . . . . 8 7 9 . . . |
$$ | . . . , . . . . . , . . . . 6 , 1 . . |
$$ | . . 5 . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . 3 . . . . . , . . . . . 4 . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]
Nothing remarkable yet; a pretty normal beginning. I only know how to place numbered stones from

to

in a diagram, btw. Is there a way to go further in a single diagram?
Game 28, position 2
- Click Here To Show Diagram Code
[go]$$Wc A slightly less familiar joseki choice
$$ ---------------------------------------
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . O . . . . . . . . . O X X . . . |
$$ | . . . , . . . 3 . b . . . 1 O , X . . |
$$ | . . X . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . 2 a . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . X . . . . . , . . . . . O . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]
If one focuses narrowly on the joseki, one might play
b instead of

here, but

is a better move as it is simultaneously responding to the approach on the upper left stone.
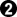
is a joseki choice I see fairly often from KataGo, but I still haven't used it much myself. However, from now I intend to try it. A couple quick variations:
- Click Here To Show Diagram Code
[go]$$Bc Variation 1
$$ --------------------
$$ . . . . . . . . . . |
$$ . . . . . . . . . . |
$$ . . . . O X X . . . |
$$ . . . . O O , X . . |
$$ . . . . . . . . . . |
$$ . . . . . . 1 . . . |
$$ . . . . . . . . 3 . |
$$ . . . . . . . 2 . . |
$$ . . . . . . . . . . |
$$ , . . . . . , . . . |[/go]
Since

is on the fourth line, it doesn't securely build territory. So
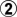
is the sort of thing that would make me nervous. However,
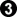
is a decent continuation that does build territory.
- Click Here To Show Diagram Code
[go]$$Bc Variation 2
$$ --------------------
$$ . . . . . . . . . . |
$$ . . . . . . . . . . |
$$ . . . . O X X . . . |
$$ . . . . O O , X . . |
$$ . . . . . . . . . . |
$$ . . . . 5 . 1 . . . |
$$ . . . . . . . 3 . . |
$$ . . . . . . 4 2 . . |
$$ . . . . . . . . . . |
$$ , . . . . . , . . . |[/go]
The kosumi-tsuke and jump is, however, about 0.3 points better.
Game 28, position 4
- Click Here To Show Diagram Code
[go]$$Bc Splitting the top
$$ ---------------------------------------
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . O . . . . . . . . . O X X . . . |
$$ | . . . , . . . O . 3 . . . O O , X . . |
$$ | . . X . b . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . f . . # . . . |
$$ | . . 2 . . . . . . . . . e d c . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . 1 . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . X . . . . . , . . . . . O . . . |
$$ | . . . . . . . . . . . . . a . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]
The double approach at
a is to me a more obvious move than
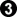
, and even receives a slightly better evaluation, but
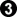
is fine and there are indeed several good moves in this position.
Now that white's three stones in the upper-right have been pincered, they will run towards the center, most likely through any of
c through
f. If black's marked stone were on the third line, white's strong preference would be for
d, but in this case these four options are all considered good.
Game 28, position 5
- Click Here To Show Diagram Code
[go]$$Wc Surround or invade?
$$ ---------------------------------------
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . O . . . . . . . . . O X X . . . |
$$ | . . . , . . . O . X . . . O O , X . . |
$$ | . . X . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . e c . . . . . X . . . |
$$ | . . O . . . . . . d . . 1 . 2 . . . . |
$$ | . . . . . . . . . . . . . . . . b . . |
$$ | . . . . . . . . . . . . . . . . a . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . X . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . X . . . . . , . . . . . O . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]
It looks a bit like white is establishing a framework on the top, which could be continued with a capping move such as
c,
d, or
e. But black is also building up the right side, so white might also like to invade with a move like
a or
b.
Game 29, position 6
- Click Here To Show Diagram Code
[go]$$Wc Running while threatening
$$ ---------------------------------------
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . O . . . . . . . . . O X X . . . |
$$ | . . . , . . . O . X . . . O O , X . . |
$$ | . . X . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . a 2 . b . . X . . . |
$$ | . . O . . . . . . . . . O . X . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . 1 . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . X . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . X . . . . . , . . . . . O . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]
White chooses to split black's moyo on the right rather than capping the black stone on the top side. Afterwards, black runs towards the center with
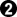
. This shape surprised me, as I would normally only think of something like
a. Actually both moves are good.
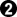
seems a bit less effective when considered purely in terms of speed towards the center, but it simultaneously threatens a splitting move at
b.
Game 29, position 7
- Click Here To Show Diagram Code
[go]$$Wc White's own splitting move
$$ --------------------
$$ . . . . . . . . . . |
$$ . . . . . . . . . . |
$$ . . . . O X X . . . |
$$ X . . . O O , X . . |
$$ . . . . . . a 1 b . |
$$ . X . . . . X 2 . . |
$$ . . . O . X . . . . |
$$ . . . . . . . . . . |
$$ . . . . . . . O . . |
$$ , . . . . . , . . . |[/go]
Ignoring black's threat, white launches an attack with

. I think I would not have even recognized this as a weak point at this point in the game.
Black's defense at
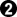
seems to be making miai of
a and
b. This is another move I probably would not have considered in favor of playing
a or
b directly. However,

has the virtue of making a connection with white's right-side stone more difficult.
- Click Here To Show Diagram Code
[go]$$Bc Variation 3
$$ --------------------
$$ . . . . . . . . . . |
$$ . . . . . a . . . . |
$$ . . . . O X X 4 . . |
$$ X . . . O O 2 X 3 . |
$$ . . . . . . 1 O . . |
$$ . X . . . . X . . . |
$$ . . . O . X . . . . |
$$ . . . . . . . . . . |
$$ . . . . . . . O . . |
$$ , . . . . . , . . . |[/go]
I was curious about what happens if black blocks on top, so I tried reading out this variation. Now white will either be able to connect on the right side or capture two stones in the corner.
I checked with KataGo, and
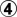
is a slight mistake compared to
a -- but still good enough to refute

.
Game 29, position 8
- Click Here To Show Diagram Code
[go]$$Wc White's connecting sequence
$$ --------------------
$$ . . . . . . . . . . |
$$ . . . . . . . . . . |
$$ . . . . O X X 2 . . |
$$ X . . . O O 1 X . . |
$$ . . . . . . 4 O 3 . |
$$ . X . . . . X X 5 . |
$$ . . . O . X . 8 6 9 |
$$ . . . . . . . . 7 . |
$$ . . . . . . . O . . |
$$ , . . . . . , . . . |[/go]
White connects with this forcing sequence. The upper right is now a tangle of weak groups and black has the opportunity to do something.
Game 29, position 9
- Click Here To Show Diagram Code
[go]$$Bc Solidifying the corner
$$ --------------------
$$ . . . . . . . . . . |
$$ . . . . . . . . . . |
$$ . . . . O X X X . . |
$$ X . . . O O O X 3 a |
$$ . . . . . . X O O 2 |
$$ . X . . . . X X O 1 |
$$ . . . O . X . X X O |
$$ . . . . . . . . O 4 |
$$ . . . . . . . O . . |
$$ , . . . . . , . . . |[/go]
First, black plays two forcing moves to help solidify the corner in sente. It would be quite reasonable to play one more move at
a, but black chooses to play that a bit later instead.
Game 29, position 10
- Click Here To Show Diagram Code
[go]$$Bc Slight mistake
$$ ---------------------------------------
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . O . . . . . . . . . O X X X . . |
$$ | . . . , . . . O . X . . . O O O X X 5 |
$$ | . . X . . . . . . . . . . . . X O O O |
$$ | . . . . . . . . . . X . . . . X X O 6 |
$$ | . . O . . . . . . . . . O . X . X X O |
$$ | . . . . . . . . . . . . . . . . . O O |
$$ | . . . . . . . . . . . . . . 3 1 O . . |
$$ | . . . , . . . . . , . . . . . 2 . . . |
$$ | . . . . . . . . . . . . . . . . 4 . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . X . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . X . . . . . , . . . . . O . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]
Next, black makes shape with

and
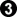
before forcing white's connection with
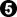
.
In review, KataGo thinks

was a slight mistake -- the
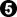

exchange should have been played first. Let's try to see why.
- Click Here To Show Diagram Code
[go]$$Bc Variation 4
$$ --------------------
$$ . . . . . . . . . . |
$$ . . . . . . . . . . |
$$ . . . . O X X X . . |
$$ X . . . O O O X X . |
$$ . . . . . . X O O O |
$$ . X . . . . X X O . |
$$ . . . O . X . X X O |
$$ . . . . . . 5 . O O |
$$ . . . . . 4 1 O 9 b |
$$ , . . . . . 2 3 7 a |
$$ . . . . . c . 6 8 . |
$$ . . . . . . . . . . |
$$ . . . . . . . . . . |
$$ . . . . . . . X . . |
$$ . . . . . . . . . . |
$$ , . . . . . O . . . |
$$ . . . . . . . . . . |
$$ . . . . . . . . . . |
$$ . . . . . . . . . . |
$$ --------------------[/go]
First let's consider what would happen if black cuts instead of extending with
. White will be able to play this sequeezing sequence, finally connecting with
a and
b and making a tiger's mouth connection with
c. This is slightly better for white than the game result.
- Click Here To Show Diagram Code
[go]$$Bc Variation 5
$$ --------------------
$$ . . . . . . . . . . |
$$ . . . . . . . . . . |
$$ . . . . O X X X . . |
$$ X . . . O O O X X 1 |
$$ . . . . . . X O O O |
$$ . X . . . . X X O 2 |
$$ . . . O . X . X X O |
$$ . . . . . . 7 . O O |
$$ . . . . . 6 3 O . . |
$$ , . . . . . 4 5 9 . |
$$ . . . . . . . 8 . . |
$$ . . . . . . . . . . |
$$ . . . . . . . . . . |
$$ . . . . . . . X . . |
$$ . . . . . . . . . . |
$$ , . . . . . O . . . |
$$ . . . . . . . . . . |
$$ . . . . . . . . . . |
$$ . . . . . . . . . . |
$$ --------------------[/go]
If black has exchanged

first, however, then white is short a liberty. Now if white tries to deal with the cut in the same way, the result would be a complete disaster.
- Click Here To Show Diagram Code
[go]$$Bc Variation 6
$$ --------------------
$$ . . . . . . . . . . |
$$ . . . . . . . . . . |
$$ . . . . O X X X . . |
$$ X . . . O O O X X 1 |
$$ . . . . . . X O O O |
$$ . X . . . . X X O 2 |
$$ . . . O . X . X X O |
$$ . . . . . . 8 . O O |
$$ . . . . . 9 3 O . . |
$$ , . . . . . 4 5 6 . |
$$ . . . . . . . 7 . . |
$$ . . . . . . . . . . |
$$ . . . . . . . . . . |
$$ . . . . . . . X . . |
$$ . . . . . . . . . . |
$$ , . . . . . O . . . |
$$ . . . . . . . . . . |
$$ . . . . . . . . . . |
$$ . . . . . . . . . . |
$$ --------------------[/go]
This is a better way of dealing with the cut. White will live small while black gets influence. However, black is still winning the game by over 9 points if this happens. Actually, being cut by
is unacceptable no matter how white plays.
- Click Here To Show Diagram Code
[go]$$Bc Variation 7
$$ --------------------
$$ . . . . . . . . . . |
$$ . . . . . . . . . . |
$$ . . . . O X X X . . |
$$ X . . . O O O X X 1 |
$$ . . . . . . X O O O |
$$ . X . . . . X X O 2 |
$$ . . . O . X . X X O |
$$ . . . . . . . . O O |
$$ . . . . . . 3 O . . |
$$ , . . . . . 5 . . . |
$$ . . . . . 7 6 4 . . |
$$ . . . . . . . . . . |
$$ . . . . . . 8 . . . |
$$ . . . . . . . X . . |
$$ . . . . . . . . . . |
$$ , . . . . . O . . . |
$$ . . . . . . . . . . |
$$ . . . . . . . . . . |
$$ . . . . . . . . . . |
$$ --------------------[/go]
Instead, white should play the one-space jump at
, resulting in this sequence where white finishes in gote locally with

. Black has gained about 0.7 points over the actual game result.
Now, if we scroll all the way back to position 10, I think we can see why

should have been at
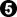
-- it makes white's hane at
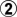
nonviable and forces white to take gote.
Game 28, position 11 (preview)
- Click Here To Show Diagram Code
[go]$$Bc White 10 at a
$$ ---------------------------------------
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . 5 4 . . 8 9 . . . |
$$ | . . . O . . . . . . 7 1 6 O X X X . . |
$$ | . . . , . . . O . X 3 2 . O O O X X X |
$$ | . . X . . . . . . . . a . . . X O O O |
$$ | . . . . . . . . . . X . . . . X X O O |
$$ | . . O . . . . . . . . . O . X . X X O |
$$ | . . . . . . . . . . . . . . . . . O O |
$$ | . . . . . . . . . . . . . . X X O . . |
$$ | . . . , . . . . . , . . . . . O . . . |
$$ | . . . . . . . . . . . . . . . . O . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . X . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . X . . . . . , . . . . . O . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]
Not sure if I'll continue the review, but here's a preview of the next few moves in case anyone's curious. I have a KGS game that I'd like to review next, so I might just move on to that.



