On winrate estimates, territory estimates, margins of error, and the last play
OC, as humans we are used to territory estimates, but we are past the hype about how top bots think differently, and better than humans, in some mysterious way about the probability of winning the game. Unless we are talking about certain situations such as the 5x5 board, where we know that the probability is 100% that Black wins with perfect play, and even reasonably good play, or the late endgame where we can figure out perfect play, or a pro vs pro game where one player leads by, say, 50 pts. and the largest play gains 10 pts., there is no a priori knowable probability of winning the game. A posteriori, we could have a position played to the end many times by certain players, or by players of comparable levels, and get winrate estimates thaty way, but we do not know how well those winrates would generalize, and to whom. In general, as the skill of the players decreases towards random play, the winrates get closer to 50%. And the bots do not estimate winrates in that manner, anyway. The mystery of winrates is baked into the cake. We really do not know enough about the factors involved. Perhaps there will be a Ph.D. dissertation about winrates in the near future.
(BTW, I have found another example where Elf is way wrong about the value of a play by a top player — Dosaku in this case. More later.
)
My purpose here is not to casts doubt on winrate estimates. They are useful. It was the hype that got me started, but that has pretty well blown over. One problem that still remains is that of their margins of error. If a top bot estimates, given sufficient playouts — and we don't know how many that is, either —, that one play has a winrate 10% worse than that of the bot's top choice, we can be pretty sure that it is a mistake. OTOH, if the winrate estimate is only 2% worse, we have little assurance that it is an error. I have recently downsized my margin of error for Elf to 4%, but that is still an educated guess. Nobody has worked out the margins of error for winrate estimates, and I doubt if anybody is going to do so anytime soon. The margin of error may be important for a human attempting to interpret winrate estimates, but any bot that picks a play with a smaller winrate estimate, given sufficient playouts, is likely to play worse. And today's bots are written to win games, not analyze positions.
Now, when we can actually work out territory estimates, we can determine the margins of error. For example, if a gote gains 5 pts., its margin of error is 5 pts., as well, since we do not know who will make the play. Assuming correct play, that is. If the players make mistakes, the margin of error could be greater. But the gain is not a territory estimate, it is something that we find out when we make the estimate. Now, some bots make territory estimates as well as winrate estimates. This is good, but, AFAIK, they do not yet estimate the margin of error of the territory estimates. In terms of the whole board the gain from making the largest gote or reverse sente is the
temperature. If we are going to use territory estimates, we need temperature estimates, as well.
That brings me to the topic of the last play. If I am 1 pt. behind and make a play that gains 3 pts., then I am 2 pts. ahead. The opponent might still win. But if my play was the last play of the game, then I win. Such a situation would be unusual, because the temperature would drop from 3 to 0, and such a large temperature drop is unusual in go. The average drop in temperature between moves is less than 1 pt. It is probably less than 0.1 pt. But larger temperature drops do occur. For instance, suppose that after my play the temperature dropped by 2 pts., i.e., to 1 pt. Then I would still (very likely) win, since I would be 2 pts. ahead and the best my opponent could do would be to gain 1 pt., not enough to catch up. (A very unusual ko situation could still give her the win, since the margin of error for ko positions is greater than their temperature.) The play just before a significant temperature drop is also called a last play.
In fact, one of the traditional dogmas of go is that of getting the last big play of the opening. Now, what that play is is not well defined, but good players can usually sense it, and sense the related temperature drop, as well. Unless the bots prove that it is hokum, which I don't think they will.
In fact, I have found an example where I think the bots back up the idea of a significant temperature drop in the opening.
It has to do with the 5-3 approach to the 3-4 point.
Now, humans have known, or at least strongly suspected, that the 5-3 approach to the 3-4 point is not as big, as a rule, as the original 3-4 play itself. Certainly by the 19th century the idea was that, usually at move 4, White should play the 5-3 approach to a 3-4 stone before occupying an empty corner, even though occupying the empty corner was better objectively, because White needed to complicate the game to overcome Black's advantage. Today, with komi, the empty corner beckons, although approaching a 3-4 stone, even at move 2, is not unknown. Writing in the mid-20th century, even Takagawa could not unequivocally say that the approach at move 2 was a mistake. Obviously, the 3-4 makes more territory, on average, but the 5-3 has more influence towards the center and the side. Which is better? Probably the 3-4, but quien sabe?
In the 17th century the 5-3 approach to the 3-4 stone was common at move 2. Did the players think that the 5-3 stone was objectively not quite as good? Maybe so, but Dosaku played a number of games as White where he played the 5-3 in all four corners, playing it as the first play in empty corners. Did he think that the 5-3 was objectively as good as, or better than, the 3-4? Obviously, he was extremely skilled at utilizing the influence of the 5-3, but would he have played it to occupy an empty corner if he were playing against himself?
Well, Elf has an opinion, expressed in terms of winrates. What does Elf say?
In a game against Yasui Chitetsu (GoGoD 1671-08-25a) Dosaku played the 5-3 approach as
against Chitetsu's 3-4
, a very common opening at the time. Elf estimates that the approach loses 5½% versus a 4-4 play in an empty corner. (I don't regard winrate estimates as precise enough to warrant reporting tenths of a point difference near 50%. Half point precision is good enough, IMHO.
) Next, Chitetsu played
as a two space pincer against
, which was also common back then. Elf regards
as a 4% winrate error. (Within decades human players had dropped the
pincer, which indicates that they also had come to regard it as an error. When both bots and humans think a play is a mistake, it probably is.
) Dosaku played
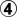
on the 5-3 in the adjacent corner closest to
. Elf considers it a 7% error. OK, Elf considers the 5-3 to be a mistake, whether as an approach to the 3-4 or as the first play in an empty corner. What does this have to do with the last play, if anything?
OK. Today's bots consider the corners to be worth more, by comparison with the sides, than humans. In the late 20th century we were starting to see humans devalue the sides by a little bit. For instance, the sanrensei was devalued, but the nirensei was still considered good. Even today, the bots like the nirensei.
But we see plays on the side that top humans played without a second thought regarded as losing 10% by today's top bots. Shoulder hits, side attachments, or other plays against enclosures are usually considered to be bigger than extensions on the side. This represents a big difference in opening theory. IOW, the temperature of the corners remains hotter than the temperature of the sides for longer than we humans have thought. A temperature drop is coming up.
GoGoD 1665-00-00a, Aoki Guseki (W) vs. Dosaku.
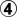
plays the 5-3 approach instead of occupying the last empty corner. Elf estimates a winrate loss of 6½%.
GoGoD 1667-12-05b, Castle Game, Honinbo Doetsu (W) vs. Yasui Chitetsu.
is a 5-3 approach, estimated loss of 5½%,
plays on the 3-4 in an open corner.
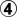
approaches on the 5-3. Estimated loss: only 2%.
(But there are two empty corners.)
GoGoD 1669-07-16, Dosaku (W) vs. Doetsu.
is a 5-3 approach. Estimated winrate loss: 6½%.
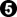
is a 5-3 approach. Estimated winrate loss: 2%. (Two empty corners.)
is a 5-3 approach instead of occupying the last empty corner. Estimated winrate loss: 7½%.
If I were writing an article or thesis, I would OC, examine many instances, either of actual games, or of computer generated positions. And I have looked at more games than I report here. The number of empty corners seems to matter to the winrate loss estimate of the 5-3 approach. Here is my hypothesis as to why.
Winrate loss estimates depend, not only upon the play made, but upon the alternative, presumably best, play. The value of the 5-3 approach in each corner is approximately the same in each case, I assume. Then the difference in winrates reflects the difference in the value of occupying an empty corner, assuming that that is the best play. When there is only one empty corner, that difference is around 6½% in terms of winrates. But when there are two empty corners, they are miai, if not exactly so. And then the difference is pretty much the loss in the corner of the 5-3 approach versus the play after the two corners are occupied, which comes to around 2%. The difference of around 4½% reflects a temperature drop after the last empty corner is occupied. Occupying the last empty corner is significant.
When there are three empty corners, there is some uncertainty about who will get to occupy the last empty corner, at least as bots calculate winrates. That uncertainty reduces the winrate estimate of the loss of the 5-3 approach by around 1½%.
OC, if I did the research I could get better estimates, and there may be other factors to consider.
But I think these results are suggestive. There does seem to be a last play effect in the opening, namely occupying the last empty corner. It comes earlier than humans have thought, but there may be another significant temperature drop a bit later on at the threshold of the middle game, and yet another at the cusp of the endgame.
Login
Register
FAQ
Search
lightvector
- 
, gains one pt., for a local score of -8.
because the local temperature has dropped below 1. Black has 6 + 1¼ = 7¼ pts. and White has 7 pts., for a net result of ¼. Black is ahead and has the move, so Black wins.
plays at 5, 
plays at 4 and wins. After 
the net result is -1½. Black can round that up to -1, but White wins.
the left side is miai, and the net result is -½, which Black can round up to 0. White does not win.
. 
Yes, I know that I have not dealt with the difficult ko position I posted, but this position, which may arise in theory, but I have never encountered across the board, is interesting in its own way, and not too difficult to evaluate.
elsewhere
, 
dame or pass
is the vital point. 
makes a one point eye. But then 
makes a Golden Cock Stands on One Leg shape, which White cannot take because of damezumari.