OK. Let's calculate the size of plays in the study.
- Click Here To Show Diagram Code
[go]$$B Black first
$$ ---------------------------
$$ | . . . . . X C W W 2 1 W C |
$$ | X X . . . X C W X O X X X |
$$ | O X X . . X X X X O O X O |
$$ | O O X , X . X O O O X X . |
$$ | . O O X . X O . . O O X . |
$$ | . 2 1 3 X O O . O O X X . |
$$ | . . O . X O X . O X X . . |
$$ | . . O X X O O O . 1 O X X |
$$ | . . O X . X O . X . O O X |
$$ | . O O O X . X O O O . . O |
$$ | . O X X X X . X O . O O . |
$$ | O X . C . . . X X O . . . |
$$ | . 1 C C . . . C 3 1 2 . . |
$$ ---------------------------[/go]
The top right is Black's 3 point sente. The threat gains 4 points.
In the bottom left
makes 3 points for Black, and the hane/connect in the bottom right makes 1 point. The other plays make no points. To calculate the gote we need to see the results if White plays first, as well.
- Click Here To Show Diagram Code
[go]$$W White first
$$ ---------------------------
$$ | . . . . . X . O O . 1 O . |
$$ | X X . . . X . O X O X X X |
$$ | O X X . . X X X X O O X O |
$$ | O O X , X . X O O O X X . |
$$ | . O O X . X O . . O O X . |
$$ | . C 1 . X O O . O O X X . |
$$ | . . O . X O X . O X X . . |
$$ | . . O X X O O O C 1 O X X |
$$ | . . O X . X O C B C O O X |
$$ | . O O O X . X O O O . . O |
$$ | C O X X X X . X O . O O . |
$$ | O B 1 2 . . . X X O . . . |
$$ | C 3 7 6 . . . 2 1 3 C . . |
$$ ---------------------------[/go]
saves the stone in the top right corner.
-
captures the
stone in the bottom left corner. Later
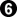
is ambiguous, but we count it like a sente. With the captured stone White makes 4 points locally. The swing is 7 points. Each play gains 3.5 points.
in the center right makes 5 points. Each play gains 2.5 points.
The hane/connect in the bottom right makes 1 point. Each play gains 1 point.
The connection on the left side makes 1 point. Each play gains 0.5 point.
These calculations give us a possible order of play, from the largest play to the smallest: Bottom left, top right, center right, bottom right, left side. That is the main line in the SGF file below.
Black wins by 0.5.
But wait! The top right is not only a local sente, it is global sente, since its threat is greater than the bottom left gote. Shouldn't Black play it first? Isn't it the right play, even if it does not change the score?
When I was doing this research, I remembered how, when I first started playing over pro games, as the game wound down, they would sometimes make haste to take their sente plays, regardless of the size of the sente. I figured it was because they knew they would not need them for ko threats, and did not want them to get away. And indeed, you can show with CGT (combinatorial game theory) that when there are no kos about, taking your global sente loses nothing to par. (I didn't know CGT at the time, but that was still obvious.
)
Variation 1 shows the result after Black plays sente in the top right and White answers. (There is a side variation when White mistakenly does not answer the sente. I included it because I think that the later play is of some interest.
) Black then takes the gote in the bottom left. Curiously, White wins by 0.5.
Well, the sente may lose nothing to par, but, as the great bridge writer Victor Mollo said, par is a poor target.
On the theory that it is easy to compare simple gote, this is the rule that I came up with to decide whether to play global sente or not, in an environment of simple gote.
Let r be the value of the reverse sente, and t0 ≥ t1 ≥ t2 ≥ . . . be how much the gote gain. t0 is the temperature of the environment.
If r < 2t1 - 2t2 + 2t3 - . . .
then do not take the sente, but take the largest gote. Note that t0 does not appear in this comparison, because the sente player gets it in either case. Since it is not part of the comparison, it is best not to consider it part of the environment, either, and consider t1 to be the ambient temperature.
In this case, 3 < 5 - 2 + 1 = 4, so my rule says to play in the bottom left. And indeed, if Black plays the sente in the top right, a loss by 0.5 is fairly predictable.
So is a 0.5 point loss the par result? Unfortunately, yes. In the main line White erred by playing the reverse sente. See the variation at move 2 for the correct play. White takes the theoretically smaller gote and wins by 0.5.
The reason that the theoretically smaller play is correct has to do with the drop in the ambient temperature after it is played. If White takes the reverse sente he gains 3 points but then loses 2 points for a net gain of 1 point, while if he takes the gote he gains 2 points, which is 1 point better. We could say that by taking the gote White gets the last play at temperature 2.5. The whole point of getting the "last play" has to do with the subsequent drop in temperature. There is nothing magical about the last play itself, or the last play of the opening, or the last play of the large endgame. It is the temperature drop that is important.
Now, I was already aware the the best move is not always the theoretically largest play. In fact, in my research I was trying to find simple rules that would tell me when not to play the theoretically largest play. Although this example is somewhat interesting and instructive, my rule does not quite fit the bill. Why not?
Because it is tantamount to reading the whole board out. To be practical, this kind of rule needs to be approximate, so that you don't have to read the whole board out. That is why the environment consists of simple gote. Few real environments consist of simple gote, but they are approximately like that. That is why the largest play is very likely to be the best play.
With approximations, the rule is really a set of possible rules:
r < t1
r < 2t1 - t2
r < 2t1 - 2t2 + t3
* * *
But with approximations come possible errors. In this case we know that playing the global sente is never technically incorrect. It is just that playing the largest gote might induce an error by our opponent. But if the rule is approximate, playing the largest gote might be an error itself.
Login
Register
FAQ
Search
Bill Spight
elsewhere
takes back at 
stone is en prise. Now we know already that this position is gote with a play gaining 1 point. Let’s continue play at temperature 1.
elsewhere
takes back at 1, 
elsewhere
are both reverses called hane-and-connect. Each reverse gains 1 point.
is a 5 move reverse that gains 1.5 points.
at 2.
is a slight inaccuracy. The solid connection is technically better. White still wins, though. 
take ko.
takes ko 
fills ko at 25. 
takes ko at 23. 
is the winning ko threat.
??
It looks like it threatens to make another point by a White play at e. However that is never going to happen because e is a ko threat for Black. So all it does is give White one more ko threat at c. But it gives Black 
at 10, and later forcing Black to take the half point on the left side before gaining one point by filling the ko. That way White gets 2 points on the bottom side, for a net score of +2. The gains and losses still add up: