Difference games (iii)
More on the second line hane. 
The second line hane occurs frequently, as does the descent on the second line. Often the difference between playing one or the other depends upon tactics. But what about when there is no particular tactical reason to choose one or the other? Let's explore that question with difference games. 
- Click Here To Show Diagram Code
[go]$$c Difference game, hane vs. descent
$$ ---------------------------------------
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . W . . . . . . . . |
$$ | X X X X X X X X X X O O O O O O O O O |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | O O O O O O O O O O X X X X X X X X X |
$$ | . . . . . . . . . B . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]
Which is better for the player to the right, the hane or the descent?
On the top side we let White play the descent, on the bottom side we let Black play the hane.
The answer is not obvious, nor is the play in the difference game, which could get complicated. Fortunately, in difference games we do not have to find the best play to win or tie; good enough play will do. 
- Click Here To Show Diagram Code
[go]$$Bc Black first
$$ ---------------------------------------
$$ | . . . . . . . . . 7 5 6 . . . . . . . |
$$ | . . . . . . . . . 1 W . . . . . . . . |
$$ | X X X X X X X X X X O O O O O O O O O |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | O O O O O O O O O O X X X X X X X X X |
$$ | . . . . . . . . 2 B 9 . . . . . . . . |
$$ | . . . . . . . . 4 8 3 . . . . . . . . |
$$ ---------------------------------------[/go]
With Black to play  is good enough to win by 3. is good enough to win by 3. 
- Click Here To Show Diagram Code
[go]$$Wc White to play
$$ ---------------------------------------
$$ | . . . . . . . . 8 7 9 . . . . . . . . |
$$ | . . . . . . . . . 2 W . . . . . . . . |
$$ | X X X X X X X X X X O O O O O O O O O |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | O O O O O O O O O O X X X X X X X X X |
$$ | . . . . . . . . 1 B 3 4 . . . . . . . |
$$ | . . . . . . . . . 5 0 6 . . . . . . . |
$$ ---------------------------------------[/go]
 fills at fills at 
 may be good enough. may be good enough.  If If 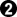 , ,  wins by 3. wins by 3.
What if Black plays the hanging connection instead. That does not look promising, but let's see.
- Click Here To Show Diagram Code
[go]$$Wc White first, variation
$$ ---------------------------------------
$$ | . . . . . . 6 3 9 5 . . . . . . . . . |
$$ | . . . . . . . 4 . 0 W . . . . . . . . |
$$ | X X X X X X X X X X O O O O O O O O O |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | O O O O O O O O O O X X X X X X X X X |
$$ | . . . . . . . . 1 B . . . . . . . . . |
$$ | . . . . . . . . 7 8 2 . . . . . . . . |
$$ ---------------------------------------[/go]
White wins by 2.
The first player wins the difference game, which means that whether to play the hane or the descent depends upon what's on the rest of the board.
----
Some time ago I noted that the hane-and-connect on the second line was fairly usual play, but that the descent was normally sente. That being the case, if you foresee that your opponent can get the hane-and-connect, why not forestall that by playing the descent with sente? Furthermore, by symmetry, that is so for both players, so normally shouldn't one player or the other play the descent with sente? In that case, we should see the pros make a lot of double descents on the second line, but we don't.  OC, tactics often matter, but still. . . . OC, tactics often matter, but still. . . .
However, if you play the hane you do not necessarily have to connect, even when tactics don't matter. What do difference games tell us about playing the hane with sente versus doing nothing? 
- Click Here To Show Diagram Code
[go]$$c Difference game, sente hane vs. no play
$$ ---------------------------------------
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | X X X X X X X X X X O O O O O O O O O |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | O O O O O O O O O O X X X X X X X X X |
$$ | . . . . . . . . W B . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]
- Click Here To Show Diagram Code
[go]$$Bc Black first
$$ ---------------------------------------
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . 1 . . . . . . . . . |
$$ | X X X X X X X X X X O O O O O O O O O |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | O O O O O O O O O O X X X X X X X X X |
$$ | . . . . . . . . W B . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]
With Black to play, the descent is good enough to win. If White responds on the top side with a descent, Black connects on the bottom side. OTOH, if White captures the Black stone on the bottom side with gote, Black plays the monkey jump on the top side.
- Click Here To Show Diagram Code
[go]$$Wc White first
$$ ---------------------------------------
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . 1 . . . . . . . . |
$$ | X X X X X X X X X X O O O O O O O O O |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | O O O O O O O O O O X X X X X X X X X |
$$ | . . . . . . . . W B . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]
With White to play, the descent is also good enough to win. If Black responds with a descent on the top side, White captures the Black stone on the bottom side. OTOH, if Black saves the Black stone, White plays the monkey jump.
The upshot of it is this. Sometimes you play the descent to prevent your opponent from playing the hane, sometimes you play the hane with sente to prevent your opponent from playing the descent, and sometimes you wait.  I suppose that sometimes you play the hane-and-connect, but I think that with enough foresight you pick one of the sente options, or your opponent will. I suppose that sometimes you play the hane-and-connect, but I think that with enough foresight you pick one of the sente options, or your opponent will.
|
 is sente, leaving White with 1 point of territory after
is sente, leaving White with 1 point of territory after  . The result is 0 with Black to play, so Black loses. If now
. The result is 0 with Black to play, so Black loses. If now  and
and 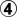 , Black can resign.
, Black can resign. is reverse sente, leaving White with 1 point of territory. The net score is 0, so Black to play loses, as above.
is reverse sente, leaving White with 1 point of territory. The net score is 0, so Black to play loses, as above. stone in it to live, it would be worth two points of territory. That is, White could take one move to capture the
stone in it to live, it would be worth two points of territory. That is, White could take one move to capture the  threatens to play at "a", making a point of territory. In fact. "a" and "b" are miai. The end result is a net local score of 0.
threatens to play at "a", making a point of territory. In fact. "a" and "b" are miai. The end result is a net local score of 0. is a better play for White.
is a better play for White. , as the rest is miai. White wins by one point.
, as the rest is miai. White wins by one point.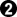 .
. 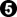 and plays at 6, hoping that White will connect and then Black can go back and play at 5?
and plays at 6, hoping that White will connect and then Black can go back and play at 5? fills the ko at
fills the ko at  fills at
fills at  White is obviously one point ahead, and wins.
White is obviously one point ahead, and wins. White obviously wins.
White obviously wins.  makes mirror go, to win.
makes mirror go, to win. , which are miai.
, which are miai. makes a zero game and wins.
makes a zero game and wins. is sente, we assume that Black will be able to play it sometime after
is sente, we assume that Black will be able to play it sometime after  is sente. White has 7 pts. in the very corner instead of 6. I believe that this is what Haylee meant by "one point better".
is sente. White has 7 pts. in the very corner instead of 6. I believe that this is what Haylee meant by "one point better".  does not gain anything to its right.
does not gain anything to its right.  at "b"
at "b"