John Fairbairn wrote:
Quote:
JF: One of the many nice things about O's book is that he explains everything without relying on terms like reverse sente (though he does mention them in passing), and you don't need to know whether there's an R in the month to know which meaning sente has.
Bill: At least in the first part of the book he only talks about local sente in local diagrams, so he is clear about that. I don't think that that is unusual. He does not define sente, however, but trusts the reader to "get it". Of course he relies upon terms like reverse sente (gyaku yose), and not just in passing.
Bill: I know you've read the book so this is for those who haven't.
Thank you for this comprehensive reply.

But truth to say, I have not read the whole book. I mean, at this point, please.

The last yose text I read in toto was Kano's
Yose Dictionary. And I made a mistake, as you point out. O did define local sente. Incorrectly, but close enough.

John Fairbairn wrote:
The reason I expressed myself the way I did is that O said (about a third of the way deep into the book):
O Meien wrote:
I would like now to continue talking about boundary plays in sente, boundary plays in gote and boundary plays in reverse sente.
If this had been a traditional endgame book, these would have come at the very beginning, but in this book we have deferred their appearance considerably.
Yes. Typically yose texts begin with sente and gote, which are and remain ill defined. One reason for that is that they need those concepts to determine the territorial count of non-final positions. Sente and gote positions have different characteristics, which lead to different ways of determining their territorial counts.
O Meien wrote:
The reason is that it is impossible to talk about boundary plays in sente, boundary plays in gote and boundary plays in reverse sente if we skirt around the factor of “value of the move.” The right approach is first to understand “value of the move” and only then talk about the various kinds of boundary play.
You end up with a kind of conundrum. You understand sente and gote in terms of the value of one move. But you find the value of one move by comparing the territorial counts of two positions. And you cannot find the territorial counts of positions without understanding sente and gote.
There are a couple of ways out of this conundrum. But first, let me say how O deals with it. First, he starts with gote positions. They are the easiest to understand. Later, on p. 43, he shows a sente position (Q). He shows a sente sequence in that position,

-
(Diagram 42), and say that

利いています。(IMO that's go jargon, and an OK translation is
is forcing.) O relies upon the notion of sente but doesn't call it that.
One way out of the conundrum, which I discovered back in the '70s, is to start off assuming that everything is gote, until you discover that it isn't. What you find is that the reply to a move is larger than it would be if the move were gote. One way to describe that is to say that the initial move raised the local temperature. Now, raising the local temperature is not enough to make a play sente. Play continues until the temperature drops below what it was to start with. (How to determine that: You keep making the assumption that each play in the sequence is the last, and keep going if you can show that it isn't.) If the last play in that sequence of play was by the second player, that sequence is sente. If the last play was by the first player, the sequence is gote. (We'll get around to
ambiguous later.

) Edit: You cannot decide whether a play is sente or gote without considering the other play, which will be either gote or reverse sente. O does not do that for that position.
Perhaps your eyes, or the eyes of other readers, glazed over when reading that. I submit that that is not the result of mathlish, even if the term
temperature is unfamiliar. The thing is, sente is not an easy concept. We have an intuitive feel for sente which is usually right, and that is good enough for most practical purposes. The difficulty with sente is not mathlish, it is inherent in the concept. (The concept would not be difficult if there were no long sente or gote sequences.)
Another way out of the conundrum was discovered by mathematicians in the mid-20th century, in relation to evaluating game positions in general, called the mean value theorem. The go concept of miai fits perfectly into the mean value theorem. If you have some number, N, of a position such that the total score, S, of all of them together is the same, regardless of who plays first (they are miai), then the average value of each of them is S/N. That works for gote positions.

The only yose text I have seen that makes use of miai in that way is in Nogami and Shimamura's book, 囲碁大観. Only for two positions, but it's a start.

For sente positions and some gote positions you don't get miai, but you can show that adding a certain number of positions, M, often just one, increases the total score by a constant, C. We can take C/M as the average value of each position. This is what I call the method of multiples. An article using this method was published in the
Deutsche Go Zeitung in the 1990s or early 2000s. The author consulted with me on the article.
I don't know if that caused any eyes to glaze over, but the concept of sente is a bit less difficult. Multiple copies of sente positions do not form miai. That's not all there is to it, however.
There is another way out of this conundrum, discovered in the 1970s by John Conway: thermography. Thermography is a practical, graphical way of finding both the value of a game or game position and the value of a move from that position at the same time.

In 2000 I presented a paper that defined sente and gote in terms of (non-ko) thermographs. It's easy.

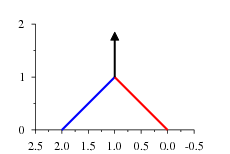
Here is a gote thermograph.
Attachment:
 gote01b.png [ 2.43 KiB | Viewed 5208 times ]
gote01b.png [ 2.43 KiB | Viewed 5208 times ]
The left wall, colored blue, indicates the result of minimax play at each temperature when Black plays first. Since Black takes gote near the top, the more that the reply in the environment gains, so the net result is less. That's why the line inclines to the right.
Similarly, the right wall, colored red, indicates the result of minimax play at each temperature when White plays first. White also takes gote, and so the right wall inclines to the left.
When the two lines meet, neither player makes a net gain from playing first, and so they are indifferent between taking the gote or not. At higher temperatures neither player will want to take the gote, which the black mast indicates. The mast rises vertically forever.
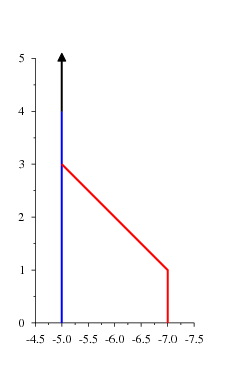
Here is a sente thermograph.
Attachment:
 sente 03.png [ 3.66 KiB | Viewed 5208 times ]
sente 03.png [ 3.66 KiB | Viewed 5208 times ]
This is a Black sente. Because White replies to Black's sente, the left wall is vertical near the top. But when White plays the reverse sente, Black does not reply and White takes gote, so the right wall looks the same as that of a gote thermograph near the top.
In addition, the mast is colored blue up to temperature 4, in this case. It takes its color from the fact that the reply to it has a higher temperature than the position itself. The color represents the privilege of sente, i.e., the fact that Black will normally be able to take the sente before White is able to play the reverse sente. If the mast is not colored, then the position is ambiguous.

Back in the '90s I had hoped that by now yose books would routinely contain at least one thermograph or two. {sigh}
Enough! For now, anyway.
Edited for correctness and, I hope, clarity.




