This 'n' that

Bill Spight · **#741**

Knotwilg wrote:

Bill, I find the argument you offer against the hypothesis of overconcentration flawed. Whatever the concept, if the opponent bot answers it's because they judge that not answering locally is even worse. That doesn't mean they are not forced into some degree of overconcentration.

Well, to quote, more or less, from ancient memory, Lasker's Chess Primer, "We have not made a mistake. There must be a good reply." If a player can be forced into overconcentration, it must be because of a previous error. Now, in this case, arguably the previous error is the keima enclosure instead of a large knight's enclosure or a two space high enclosure. So you make a good point for :w10:

in the earlier diagram. However, forcing overconcentration cannot be a general strategy unless your opponent consistently makes the right kind of errors.

Quote:

That's the whole point of sente, regardless of the underlying concept: you play a move because you think the opponent should answer locally and you think it gives you some benefit. When the opponent answers, that can still be his best move. And that in turn doesn't mean the sente was wrong.

Sure. But we don't say that the reply to the sente gets a bad result, either, i.e., kikasare. Fair is fair.

Quote:

Many concepts would lose their meaning, like "shape", if refusing to be coerced into it, like "bad shape", were always better than allowing for it.

Well, yes, I love to give my opponents bad shape. But, again, that depends upon their having made a previous error that I can recognize. It doesn't happen that often.

Edit: While forcing the opponent to make bad shape cannot be a general strategy, at least on the dan level, preventing the opponent from making good shape can be. It seems to me that the bots' top choices are often those that, while not forcing bad shape or overconcentration on the opponent, prevent the opponent from making good shape. When I note a shape play by a bot, it is usually of that sort, rather than making good shape itself.

Bill Spight · **#742**

And on the topic of high flying AI moves, here is another one.

Click Here To Show Diagram Code: [go]$$Wcm16 Elf's variation for $$ --------------------------------------- $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . O X 1 . . . . . . O X X . . . | $$ | . . . O . O . . . X . . . O O , X . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . O . . . . . . . . . . . . X . . . | $$ | . . . . . . . . . . 2 . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . , . . . . . , . . . . . , . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . X , . . . . . , . . . . . X . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ ---------------------------------------[/go]

Like LZ, Elf likes the strong :w16:

. But then it recommends the high flying large knight's jump.

Beautiful, isn't it?

John Fairbairn · **#743**

Quote:

Bill, I find the argument you offer against the hypothesis of overconcentration flawed. Whatever the concept, if the opponent bot answers it's because they judge that not answering locally is even worse. That doesn't mean they are not forced into some degree of overconcentration.

That's the whole point of sente, regardless of the underlying concept: you play a move because you think the opponent should answer locally and you think it gives you some benefit. When the opponent answers, that can still be his best move. And that in turn doesn't mean the sente was wrong.

I was going to comment on Bill's point, too, though not to counter it, at least not in such a direct way. In fact, in a quite diffident way. If we call these negotiations "overconcentration fights" for want of an existing term, what I have noticed about them is the peculiar way they stop, start and jerk about. It is not a smooth process, and my guess is that what we are seeing is, here too, a series of moves predicated on getting them in the right order, or well timed in other ways. I speculate that what may be happening on the grand scale is that time is becoming a much bigger element in go then ever before. Up to now it has been dominated by shape, in all its guises.

A further way of characterising it that often comes to me (because it makes such a strong impression on me when I see it) is that it's like the difference between Rembrandt and Picasso. Or between classical ballet and modern dance. In short, there's an abstract jerkiness.

Kirby · **#744**

Bill Spight wrote:

And on the topic of high flying AI moves, here is another one.

Click Here To Show Diagram Code: [go]$$Wcm16 $$ --------------------------------------- $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . O X 1 . . . . . . O X X . . . | $$ | . . . O . O . . . X . . . O O , X . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . O . . . . . . . . . . . . X . . . | $$ | . . . . . . . . . . 2 . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . , . . . . . , . . . . . , . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . X , . . . . . , . . . . . X . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ ---------------------------------------[/go]

Like LZ, Elf likes the strong :w16:

. But then it recommends the high flying large knight's jump.

Beautiful, isn't it?

I like that move. When I look at the position with whatever version of KataGo I have, that's one of the moves katago explores, too. Then it starts to favor the small knight's move:

Click Here To Show Diagram Code: [go]$$Wcm16 $$ --------------------------------------- $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . O X 1 . . . . . . O X X . . . | $$ | . . . O . O . . . X . . . O O , X . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . O . . . . . . . 2 . . . . X . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . , . . . . . , . . . . . , . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . X , . . . . . , . . . . . X . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ ---------------------------------------[/go]

and then after a little while (I stopped watching after 10k playouts), it recommends this:

Click Here To Show Diagram Code: [go]$$Wcm16 $$ --------------------------------------- $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . O X 1 . . . . . . O X X . . . | $$ | . . . O . O . . . X . . . O O , X . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . O . . . . . . . . . . 2 . X . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . , . . . . . , . . . . . , . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . X , . . . . . , . . . . . X . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ ---------------------------------------[/go]

The last one kind of makes sense to me - it establishes a good position on the right. So I looked at some of the follow-ups for the large knight's you posted, along with the small knight's move. In both cases, it seemed to think that white would jump out, and then black could tenuki and enclose the bottom left:

Click Here To Show Diagram Code: [go]$$Wcm16 $$ --------------------------------------- $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . O X 1 . . . . . . O X X . . . | $$ | . . . O . O . . . X . . . O O , X . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . O . . . . . . . . . . . . X . . . | $$ | . . . . . . . . . . 2 . . 3 . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . , . . . . . , . . . . . , . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . X , 4 . . . . , . . . . . X . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ ---------------------------------------[/go]

If I actually play out the large knight's move, it adjusts a bit, and then white gets to play in the bottom left first:

Click Here To Show Diagram Code: [go]$$Wcm16 $$ --------------------------------------- $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . O X 1 . . . . 4 . O X X . . . | $$ | . . . O . O . . . X 6 5 . O O , X . . | $$ | . . . . . . . . . . . 7 . . . . . . . | $$ | . . O . . . . . . 8 . . . . . X . . . | $$ | . . . . . . . . . . 2 . 3 . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . , . . . . . , . . . . . , . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . X , . . . . . , . . . . . X . . . | $$ | . . . . 9 . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ ---------------------------------------[/go]

White the smaller knight's move, even after I play it, I guess white doesn't have the same kind of forcing move against it, so it still recommends for white to jump out:

Click Here To Show Diagram Code: [go]$$Wcm16 $$ --------------------------------------- $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . O X 1 . . . . . . O X X . . . | $$ | . . . O . O . . . X . . . O O , X . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . O . . . . . . . 2 . . . . X . . . | $$ | . . . . . . . . . . . . . 3 . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . , . . . . . , . . . . . , . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . X , . . . . . , . . . . . X . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ ---------------------------------------[/go]

And then black can play in the bottom left again.

My thought here is that the bottom left approach/enclosure is somewhat big, so one possible idea for black is to strengthen his single stone on top a bit, and enclose the bottom left.

If that's true, then why not just enclose the bottom left first? If I try that...

Click Here To Show Diagram Code: [go]$$Wcm16 $$ --------------------------------------- $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . O X 1 . . . . . . O X X . . . | $$ | . . . O . O . . . X . . . O O , X . . | $$ | . . . . . . . . . . 3 . . . . . . . . | $$ | . . O . . . . . . . . . . . . X . . . | $$ | . . C . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . , . . . . . , . . . . . , . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . X , 2 . . . . , . . . . . X . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ ---------------------------------------[/go]

KataGo doesn't even recommend that black responds to the 5th line shoulder hit, instead, favoring the tenuki at the marked intersection on the left. I suppose white is strong in the area, so there may be some disadvantage to continuing there....

So maybe black aims to get a group that can't be strongly attacked, then move to the big area in the bottom left quickly?

Bill Spight · **#745**

John Fairbairn wrote:

If we call these negotiations "overconcentration fights" for want of an existing term, what I have noticed about them is the peculiar way they stop, start and jerk about. It is not a smooth process, and my guess is that what we are seeing is, here too, a series of moves predicated on getting them in the right order, or well timed in other ways. I speculate that what may be happening on the grand scale is that time is becoming a much bigger element in go then ever before. Up to now it has been dominated by shape, in all its guises.

Interesting idea.

I recall the Elf team saying that it learned to play the endgame first, which makes sense in unsupervised training. And the endgame, once the board is divided into independent regions, typically makes a move or two in one region, then switches to another region where the play has become more important, and so on. What if zero bots view the board, not as fully independent regions, but as quasi-independent regions? Then play would develop in a similar fashion, a few plays here, a few plays there, and so on and so forth. Play might start in the corners, and then it might take a while for the sides to become important. In such play the corners might appear to us humans, who are not used to such a way of playing, to become a bit overconcentrated before play widened to the sides and center.

John Fairbairn · **#746**

Quote:

KataGo doesn't even recommend that black responds to the 5th line shoulder hit, instead, favoring the tenuki at the marked intersection on the left.

This is a conventional way of describing the situation which maybe close to 100% of us would use.

But it has consequences. If a guy hits us we hit back, right? Or if he's too strong we run away. Whatever we do, we respond. That's implied in a "hit".

Bots don't have those hang-ups.

Can I suggest you might find a vastly different way of seeing these situations if you don't say "shoulder hit" but "shoulder probe"? And that that may give you more of bot's eye view.

After all, in real life we "respond" quite differently to a hit on the shoulder and a tap on the shoulder. Would we respond at all to a "look" at our shoulder? I suspect our reaction would be: "What's he up to?" And if he's a Minneapolis cop, we think: "Tenuki, fast!"

ez4u · **#747**

I realize that the discussion of this position has finished but I only today have had time to post some interesting insights from running katago on the earlier position.

All of the following is based on calculations using the katago 20-block (my hardware limitations) with Japanese rules and analysisWideRootNoise = 0.03 (my new standard = moderate diversity in search). In this case I also set komi to zero.

Bill Spight wrote:

The four enclosure position is from a 19th century game, but could arise today. Black has fallen behind, because of the two tight enclosures.

In the game Black played :b9:

at a, the traditional extension between facing enclosures, but the shoulder play (b)is modern AI style...

It turns out that the 20b calculates blue as the slightly wider extension at c below. This is true at 10K playouts and persists at 200K (the limit of my patience).

Both b and a are nearly as highly regarded. That is not the interesting point. IMHO the interesting lesson from katago is how we should think about playing against the small knight enclosure.

Click Here To Show Diagram Code: [go]$$Bcm9 A classic fuseki $$ --------------------------------------- $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . O . . . . . . . . . . X . . . . | $$ | . . . , . . . . . , . . . . . , X . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . O . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . , . . . . . , . . . . . , a . . | $$ | . . . . . . . . . . . . . . . . c . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . X . . . . . . . . . . . . . . . . | $$ | . . . , . . . . . . . . . b . , O . . | $$ | . . . X . . . . . . . . . . O . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ ---------------------------------------[/go]

Most of us (and virtually all of us who took up the game before alphago?) have seen a diagram like the following in this or that fuseki book. The explanation is that :b9:

allows Black to build on a larger scale than White.

Click Here To Show Diagram Code: [go]$$Bcm9 A classic fuseki $$ --------------------------------------- $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . O . . . . . . . . . . X . . . . | $$ | . . . , . . . . . , . . . . . , X . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . O . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . , . . . . . , . . . . 3 , 1 . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . 4 . 2 . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . X . . . . . . . . . . . . . . . . | $$ | . . . , . . . . . . . . . . . , O . . | $$ | . . . X . . . . . . . . . . O . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ ---------------------------------------[/go]

Katago sees it a little differently. Whether Black extends all the way to R9 below or holds back to R10 as above (with White responding at either R8 or R7), Black answers a White extension by immediately attaching at O3. GoGoD turns up no examples of this pattern among us mere mortals.

Click Here To Show Diagram Code: [go]$$Bcm9 Katago will attach next $$ --------------------------------------- $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . O . . . . . . . . . . X . . . . | $$ | . . . , . . . . . , . . . . . , X . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . O . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . , . . . . . , . . . . . , a . . | $$ | . . . . . . . . . . . . . . . . 1 . . | $$ | . . . . . . . . . . . . . . . . b . . | $$ | . . . . . . . . . . . . . . . . 2 . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . X . . . . . . . . . . . . . . . . | $$ | . . . , . . . . . . . . . . 7 , O . . | $$ | . . . X . . . . . . 9 . 5 3 O 8 . . . | $$ | . . . . . . . . . . . . 6 4 . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ ---------------------------------------[/go]

Katago calculates that White does best to respond to the original extension. The reason is another attachment. In lines where White plays elsewhere, for example extending at the top, katago favors the immediate attachment at R5 below.

Click Here To Show Diagram Code: [go]$$Bcm9 Katago will attach next here too! $$ --------------------------------------- $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . O . . . . . . . . . . X . . . . | $$ | . . . , . . . . . 2 . . . . . , X . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . O . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . , . . . . . , . . . . . , a . . | $$ | . . . . . . . . . . . . . . . . 1 . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . X . . . . . . . . . . . . . 3 . . | $$ | . . . , . . . . . . . . . . . , O . . | $$ | . . . X . . . . . . . . . . O . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ | . . . . . . . . . . . . . . . . . . . | $$ ---------------------------------------[/go]

I was excited by this "idea" that the power of the initial extension comes from the ability to exploit the tightness of the small knight enclosure by attaching on one side or the other. It is something not on my personal radar screen at all, up to now. The extensions have been around for centuries as the answer to "what's the next move" fuseki problems. But we may have to rewrite some of those "read the next 3 moves" problems.

Bill Spight · **#748**

Thanks, Dave! That's great stuff. Verrrrry interesting.

BTW, the game was 1844-10-09a, between Honinbo Shuwa (W) and Yasui Sanchi IX, both 7 dan.

Bill Spight · **#749**

Now for something easy.

Click Here To Show Diagram Code: [go]$$B Evaluate $$ ---------------- $$ . O X X X X . . . $$ . O C C C X X . . $$ . O B B B C X X . $$ . O O O O B O X . $$ . . . . O O O X . $$ . . . . . . . . .[/go]

What's the territorial count for the marked points and stones?

How much does a play gain?

Enjoy!

Bill Spight · **#750**

Click Here To Show Diagram Code: [go]$$B Evaluate $$ ---------------- $$ . O X X X X . . . $$ . O C C C X X . . $$ . O B B B C X X . $$ . O O O O B O X . $$ . . . . O O O X . $$ . . . . . . . . .[/go]

What's the territorial count for the marked points and stones?

How much does a play gain?

---------------------------

This is easy, so I'll just hide the solution without waiting for anyone to respond.

OK, here goes.

Bill Spight · **#751**

OT, but good news.

The BBC reports that the steroid dexamethasone has been shown to reduce the risk of death by Covid-19.

ez4u · **#752**

Bill Spight wrote:

OT, but good news.

The BBC reports that the steroid dexamethasone has been shown to reduce the risk of death by Covid-19.

Banned for sports people, including mind-gamers of course! :blackeye:

Bill Spight · **#753**

No point in hiding this.

Let Black be komonster, not only able to win the ko but able to keep fighting it until the ambient temperature is 0. Temperature 0 by area scoring is -1 by chilled area scoring. I.e., if you are komonster at territory scoring you don't have to win the ko until the dame stage; at area scoring you don't have to win the ko until the stage of filling territory or passing.

1) Territory scoring.

Click Here To Show Diagram Code: [go]$$B Black first $$ ---------------- $$ . O X X X X . . . $$ . O 1 C C X X . . $$ . O X X X . X X . $$ . O O O O X O X . $$ . . . . O O O X . $$ . . . . . . . . .[/go]

Result: 2 pts.

Click Here To Show Diagram Code: [go]$$W White first, Black reply $$ ---------------- $$ . O X X X X . . . $$ . O 1 2 C X X . . $$ . O X X X . X X . $$ . O O O O X O X . $$ . . . . O O O X . $$ . . . . . . . . .[/go]

Result: 1 pt.

Click Here To Show Diagram Code: [go]$$W White - White $$ ---------------- $$ . O X X X X . . . $$ . O 1 3 . X X . . $$ . O X X X . X X . $$ . O O O O X O X . $$ . . . . O O O X . $$ . . . . . . . . .[/go]

Result: 0

All of which means that the original territorial count is 1¼ and each play gains ¾ pt.

2) Chilled Area scoring, counting territory

Click Here To Show Diagram Code: [go]$$B Black first $$ ---------------- $$ . O X X X X . . . $$ . O 1 C C X X . . $$ . O X X X C X X . $$ . O O O O X O X . $$ . . . . O O O X . $$ . . . . . . . . .[/go]

Result: 3 pts.

Click Here To Show Diagram Code: [go]$$W White first, Black reply $$ ---------------- $$ . O X X X X . . . $$ . O 1 2 C X X . . $$ . O X X X C X X . $$ . O O O O X O X . $$ . . . . O O O X . $$ . . . . . . . . .[/go]

Result: 2 pts.

Click Here To Show Diagram Code: [go]$$W White - White - Black $$ ---------------- $$ . O X X X X . . . $$ . O 1 3 4 X X . . $$ . O X X X C X X . $$ . O O O O X O X . $$ . . . . O O O X . $$ . . . . . . . . .[/go]

Result: 1 pt.

Click Here To Show Diagram Code: [go]$$W White - White - White - Black $$ ---------------- $$ . O X X X X . . . $$ . O 1 3 5 X X . . $$ . O X X X 6 X X . $$ . O O O O X O X . $$ . . . . O O O X . $$ . . . . . . . . .[/go]

Result: 0

Which means that the chilled area count after :w1:

-

is 0, with reverse sente by Black gaining 1 pt. of territory.

Which means that the chilled area count after :w1:

is 1; the position is ambiguous with local temperature 1.

Which also means that the original chilled area count is 2; the position is ambiguous with local temperature 1.

Bill Spight · **#754**

No point in hiding this, either.

This time let White be komonster.

1) Territory scoring.

Click Here To Show Diagram Code: [go]$$B Black first, White second $$ ---------------- $$ . O X X X X . . . $$ . O 1 C C X X . . $$ . O X X X 2 X X . $$ . O O O O B O X . $$ . . . . O O O X . $$ . . . . . . . . .[/go]

Result: 1 pt.

Click Here To Show Diagram Code: [go]$$B Black - Black $$ ---------------- $$ . O X X X X . . . $$ . O 1 C C X X . . $$ . O X X X 3 X X . $$ . O O O O X O X . $$ . . . . O O O X . $$ . . . . . . . . .[/go]

Result: 2 pts.

Which means that the territorial count after :b1:

closing the corridor is 1½.

Click Here To Show Diagram Code: [go]$$B Black first, filling ko $$ ---------------- $$ . O X X X X . . . $$ . O C C C X X . . $$ . O X X X 1 X X . $$ . O O O O X O X . $$ . . . . O O O X . $$ . . . . . . . . .[/go]

Result: 1¼.

This is ¼ pt. less than closing the corridor. As if we didn't know.

Click Here To Show Diagram Code: [go]$$W White - Black - White(ko) $$ ---------------- $$ . O X X X X . . . $$ . O 1 2 C X X . . $$ . O X X X 3 X X . $$ . O O O O B O X . $$ . . . . O O O X . $$ . . . . . . . . .[/go]

Result: 0

Click Here To Show Diagram Code: [go]$$W White - Black(ko) - White $$ ---------------- $$ . O X X X X . . . $$ . O 1 3 . X X . . $$ . O X X X 2 X X . $$ . O O O O X O X . $$ . . . . O O O X . $$ . . . . . . . . .[/go]

Result: 0

Which means that after :w1:

in the corridor, the play in the corridor and the play in the ko are miai. Which means that the result after :w1:

in the corridor is 0.

Click Here To Show Diagram Code: [go]$$W White first, taking ko $$ ---------------- $$ . O X X X X . . . $$ . O 3 4 C X X . . $$ . O X X X 1 X X . $$ . O O O O B O X . $$ . . . . O O O X . $$ . . . . . . . . .[/go]

After

,

is ambiguous at temperature 1. Result: 0.

However, :b2:

could be at 3, gaining 1 pt. So correct play for :w1:

is to enter the corridor.

All of which means that the territorial count of the original position is ¾ pt., with each play gaining ¾ pt.

2) Chilled area scoring.

Now, the temperature of the ko by itself is 1 when White is komonster, which is the maximum in the corridor by itself, so it makes sense to start with play in the ko. We try that first.

Click Here To Show Diagram Code: [go]$$B Black(ko) $$ ---------------- $$ . O X X X X . . . $$ . O C C C X X . . $$ . O X X X 1 X X . $$ . O O O O X O X . $$ . . . . O O O X . $$ . . . . . . . . .[/go]

Result: 1¼ pts.

Click Here To Show Diagram Code: [go]$$B Black (corridor) - White $$ ---------------- $$ . O X X X X . . . $$ . O 1 C C X X . . $$ . O X X X 2 X X . $$ . O O O O B O X . $$ . . . . O O O X . $$ . . . . . . . . .[/go]

Result: 0

We know that :w2:

gains 1 pt., so the result after :b1:

in the corridor is 1. So :b1:

should fill the ko, as if we didn't know.

Click Here To Show Diagram Code: [go]$$W White(ko) - Black $$ ---------------- $$ . O X X X X . . . $$ . O 2 C C X X . . $$ . O X X X 1 X X . $$ . O O O O B O X . $$ . . . . O O O X . $$ . . . . . . . . .[/go]

Result: 0.

Click Here To Show Diagram Code: [go]$$W White - White - Black $$ ---------------- $$ . O X X X X . . . $$ . O 3 4 C X X . . $$ . O X X X 1 X X . $$ . O O O O B O X . $$ . . . . O O O X . $$ . . . . . . . . .[/go]

Result: -1 pt.

After :w1:

takes the ko, :w3:

is ambiguous, so the result after :w1:

is -1.

Putting it all together, the original chilled area count is ⅛, with each play gaining 1⅛.

Bill Spight · **#755**

On presentation

Click Here To Show Diagram Code: [go]$$B Evaluate $$ ---------------- $$ . O X X X X . . . $$ . O C C C X X . . $$ . O B B B C X X . $$ . O O O O B O X . $$ . . . . O O O X . $$ . . . . . . . . .[/go]

BTW, for this problem I tried the idea of indicating possible (later, actual) territory and potentially capturable (later, captured) stones. Was doing so a help or an annoyance or distraction?

Bill Spight · **#756**

On the calculation of variations

As my readers know, I don't usually say much about the conscious calculation of variations. I usually mention seeing, which is the conscious result of unconscious calculation. Seeing is not the same as having a so-called policy network, although seeing, like conscious calculation, depends upon the choice of which plays to explore.

But recently I have gotten interested in taking another look at human calculation of variations. Conscious calculation is severely limited by the size of human cortical workspace, so pretty much has to be based on depth first search.

Part of this interest has been inspired by a couple of topics here on Life in 19x19. One is Knotwilg's topic, Complexity as width x depth ( https://www.lifein19x19.com/viewtopic.php?f=15&t=17682 ). Another is BadukDoctor's topic, Daily life and death training ( https://www.lifein19x19.com/viewtopic.php?f=12&t=17284 ). To quote jlt about the latter:

jlt wrote:

I like this series (as well as other videos of BadukDoctor). Not only he shows various techniques that occur in capturing races and life-and-death problems, but also he illustrates quite well his recommended method of practicing go problems: read all variations until the end even if they don't seem to work; try other moves even if we found a way to live or kill.

OC, reading to the end makes use of depth first calculation, and trying other moves emphasizes exploration. The idea is not just to solve a problem, but to understand it thoroughly.

One way of combining depth first search with exploration is iterative deepening depth first search. I.e., reading each option to depth one, then, if a solution is not found, reading each option to depth two, etc. AFAIK, nobody has actually suggested that humans use that for game tree search, but I thought I'd take a look.

Let me create the file for iterative deepening.

Bill Spight · **#757**

Progris Riport

Well, trying to make an SGF file for iterative deepening as a whole was not a good idea. I got lost, and if I had not known the solution ahead of time I would not have know it afterwards. Easier just to do the calculations in my head. :lol:

No results until depth 3, so here is the depth 3 file for depth first search.

Hmmm. It seems that I accidentally posted this.

Let me continue.

Psychological notes.

1) Stopping after 3 moves went against the grain, unless the position was resolved.

2) Deliberately playing bad moves, except at move 1, was even worse. OC, in real life, moves we think are bad are not necessarily so. That holds for both bots and humans.

OC, raw beginners may not share these feelings.

Technical note.

Noticing transpositions is useful. One way to help do so is to keep the same order of moves for each player. That way, it is easy to tell if the order is reversed. That will usually indicate a transposition.

Possible go lessons.

I only used a 9x9 board for convenience, so I am going to leave the diagrams as 19x19.

Click Here To Show Diagram Code: [go]$$Bc White dies $$ -------------- $$ | . . . . . . . $$ | X X X X . . . $$ | . O O 1 X . . $$ | 2 . 3 O X . . $$ | O O O X X . . $$ | . O X . . . . $$ | O O X . . . . $$ | . X X . . . . $$ | . . . . . . . $$ | . . . , . . .[/go]

is a likely mistake. We can only say likely at this point, because White dying is the expected result of the problem. OC, a 5 kyu is not going to play :w2:

, but I am taking the viewpoint of a raw beginner, for whom this is a lesson.

Click Here To Show Diagram Code: [go]$$Bc White dies $$ -------------- $$ | . . . . . . . $$ | X X X X . . . $$ | . O O 3 X . . $$ | 2 . 1 O X . . $$ | O O O X X . . $$ | . O X . . . . $$ | O O X . . . . $$ | . X X . . . . $$ | . . . . . . . $$ | . . . , . . .[/go]

Transposition.

Click Here To Show Diagram Code: [go]$$Bc White dies $$ -------------- $$ | . . . . . . . $$ | X X X X . . . $$ | 3 O O 1 X . . $$ | . 2 . O X . . $$ | O O O X X . . $$ | . O X . . . . $$ | O O X . . . . $$ | . X X . . . . $$ | . . . . . . . $$ | . . . , . . .[/go]

Again,

is a likely error.

Click Here To Show Diagram Code: [go]$$Bc White dies $$ -------------- $$ | . . . . . . . $$ | X X X X . . . $$ | 1 O O 3 X . . $$ | . 2 . O X . . $$ | O O O X X . . $$ | . O X . . . . $$ | O O X . . . . $$ | . X X . . . . $$ | . . . . . . . $$ | . . . , . . .[/go]

Transposition.

Click Here To Show Diagram Code: [go]$$Bc White dies $$ -------------- $$ | . . . . . . . $$ | X X X X . . . $$ | 1 O O . X . . $$ | 3 . 2 O X . . $$ | O O O X X . . $$ | . O X . . . . $$ | O O X . . . . $$ | . X X . . . . $$ | . . . . . . . $$ | . . . , . . .[/go]

Ditto.

Click Here To Show Diagram Code: [go]$$Bc White dies $$ -------------- $$ | . . . . . . . $$ | X X X X . . . $$ | 3 O O . X . . $$ | 1 . 2 O X . . $$ | O O O X X . . $$ | . O X . . . . $$ | O O X . . . . $$ | . X X . . . . $$ | . . . . . . . $$ | . . . , . . .[/go]

Transposition.

Aside from the likelihood that :w2:

is a mistake in these variations, can we draw any other conclusions?

Samuel Butler wrote:

Life is the art of drawing sufficient conclusions from insufficient premises.

Click Here To Show Diagram Code: [go]$$Bc Where is ? $$ -------------- $$ | . . . . . . . $$ | X X X X . . . $$ | C O O C X . . $$ | M M M O X . . $$ | O O O X X . . $$ | . O X . . . . $$ | O O X . . . . $$ | . X X . . . . $$ | . . . . . . . $$ | . . . , . . .[/go]

In the six variations where White dies, :w2:

lies on each of the :ex:

points twice, but never on the :ec:

points. Which suggests that the :ec:

points are typically good points for White.

Note also that :w2:

is never adjacent to :b1:

. Which suggests that playing adjacent to :b1:

may be a good idea.

What about :b1:

?

Click Here To Show Diagram Code: [go]$$Bc Where is ? $$ -------------- $$ | . . . . . . . $$ | X X X X . . . $$ | C O O C X . . $$ | T M T O X . . $$ | O O O X X . . $$ | . O X . . . . $$ | O O X . . . . $$ | . X X . . . . $$ | . . . . . . . $$ | . . . , . . .[/go]

lies on each :ec:

point twice, on each :et:

point once, and on the :ex:

point never. Which suggests that the :ec:

points are good for Black and the :ex:

point is bad for Black.

Bill Spight · **#758**

Iterative deepening, continued

The depth 4 search was interesting. And productive. I followed the heuristic of playing :w2:

next to

, if possible, and otherwise playing on one of :ec:

points of the depth 3 search. That reduced the work quite a bit by frequently letting White live on move 4 without much search. Below is the depth 4 SGF file.

The depth 4 search revealed Black's first move. It did so by proving that White lives after each of the other first moves. The logic is simple. If, after a Black move, White has a reply that makes White live, the Black move fails to kill (or make ko, if that is the outcome). And that White move makes life if it does so by making two eyes or a seki, or if every Black reply allows White to live.

Click Here To Show Diagram Code: [go]$$Bc White lives $$ -------------- $$ | . . . . . . . $$ | X X X X . . . $$ | 2 O O 1 X . . $$ | M M M O X . . $$ | O O O X X . . $$ | . O X . . . . $$ | O O X . . . . $$ | . X X . . . . $$ | . . . . . . . $$ | . . . , . . .[/go]

After

,

lives because :w4:

can make life after :b3:

on each of the :ex:

points.

Click Here To Show Diagram Code: [go]$$Bc White lives $$ -------------- $$ | . . . . . . . $$ | X X X X . . . $$ | M O O M X . . $$ | M 2 1 O X . . $$ | O O O X X . . $$ | . O X . . . . $$ | O O X . . . . $$ | . X X . . . . $$ | . . . . . . . $$ | . . . , . . .[/go]

Ditto.

Click Here To Show Diagram Code: [go]$$Bc White lives $$ -------------- $$ | . . . . . . . $$ | X X X X . . . $$ | 2 O O M X . . $$ | 1 M M O X . . $$ | O O O X X . . $$ | . O X . . . . $$ | O O X . . . . $$ | . X X . . . . $$ | . . . . . . . $$ | . . . , . . .[/go]

Ditto.

Click Here To Show Diagram Code: [go]$$Bc White lives $$ -------------- $$ | . . . . . . . $$ | X X X X . . . $$ | M O O M X . . $$ | 2 1 . O X . . $$ | O O O X X . . $$ | . O X . . . . $$ | O O X . . . . $$ | . X X . . . . $$ | . . . . . . . $$ | . . . , . . .[/go]

After

Black has only 2 points for :b3:

, and White makes life after each one. :w2:

may not be best play, but it makes life with :w4:

. (OC, it makes life itself, but I am taking the viewpoint of a rank beginner.)

So Black's first move is the crawl along the edge at A-17.

We have already eliminated two of White's replies at depth 3, and then after each remaining :w2:

, Black has only one good reply. That leaves us with the following possibilities for depth 5.

Click Here To Show Diagram Code: [go]$$Bc Variation 1 $$ -------------- $$ | . . . . . . . $$ | X X X X . . . $$ | 1 O O 2 X . . $$ | 5 3 4 O X . . $$ | O O O X X . . $$ | . O X . . . . $$ | O O X . . . . $$ | . X X . . . . $$ | . . . . . . . $$ | . . . , . . .[/go]

Click Here To Show Diagram Code: [go]$$Bc Variation 2 $$ -------------- $$ | . . . . . . . $$ | X X X X . . . $$ | 1 O O 2 X . . $$ | 4 3 5 O X . . $$ | O O O X X . . $$ | . O X . . . . $$ | O O X . . . . $$ | . X X . . . . $$ | . . . . . . . $$ | . . . , . . .[/go]

Click Here To Show Diagram Code: [go]$$Bc Variation 3 $$ -------------- $$ | . . . . . . . $$ | X X X X . . . $$ | 1 O O 5 X . . $$ | 2 4 3 O X . . $$ | O O O X X . . $$ | . O X . . . . $$ | O O X . . . . $$ | . X X . . . . $$ | . . . . . . . $$ | . . . , . . .[/go]

Click Here To Show Diagram Code: [go]$$Bc Variation 4 $$ -------------- $$ | . . . . . . . $$ | X X X X . . . $$ | 1 O O 4 X . . $$ | 2 5 3 O X . . $$ | O O O X X . . $$ | . O X . . . . $$ | O O X . . . . $$ | . X X . . . . $$ | . . . . . . . $$ | . . . , . . .[/go]

White dies in all four cases.

Playing

next to

was a good rule of thumb.

Bill Spight · **#759**

Discussion of the problem and solution process

My guess is that this is around a 5 kyu problem. OC, a 5 kyu might well overlook the kill in an actual game, but given the position as a problem, could probably solve it in a reasonable amount of time. Hmmm. Maybe it is a 7 kyu problem.

Before posting this I went back and took another look at BadukDoctor's treatment of this problem. He was quite thorough, with attention to detail, and showed most of the same variations as I put in the depth 4 file. The problem material available in books and magazines when I was learning go usually showed only a few variations, and if I found the mainline solution I was satisfied. But some years ago I ran across Mr. K's site, http://mrkigo.sakura.ne.jp/ksikatuindex.html , where he goes into great detail about introductory life and death positions. There was a lot that I had never thought about, lessons that I had not learned at that stage in my development, but in retrospect I wish that I had learned back then. I became an instant fan of Mr. K's thoroughness.

Let's take a look at one variation.

Click Here To Show Diagram Code: [go]$$Bc White lives, depth 4 $$ -------------- $$ | . . . . . . . $$ | X X X X . . . $$ | . O O 2 X . . $$ | 4 3 1 O X . . $$ | O O O X X . . $$ | . O X . . . . $$ | O O X . . . . $$ | . X X . . . . $$ | . . . . . . . $$ | . . . , . . .[/go]

Now, for a 5 kyu, or a 7 kyu, or even most DDKs, :b3:

is silly. However, to prove that :w2:

lives, it is necessary to show that :b3:

does not kill. And, from the standpoint of learning to calculate variations, it is good to practice thoroughness and attention to detail.

At the same time, however, . . .

Click Here To Show Diagram Code: [go]$$Bc White lives this way, too $$ -------------- $$ | . . . . . . . $$ | X X X X . . . $$ | 4 O O 3 X . . $$ | . 2 1 O X . . $$ | O O O X X . . $$ | . O X . . . . $$ | O O X . . . . $$ | . X X . . . . $$ | . . . . . . . $$ | . . . , . . .[/go]

also lives, making 3 and 4 miai for life. It is not necessary, from the standpoint of solving the problem, and, hence, of calculating variations to that end, to show more than one way for :w2:

to make life. In my depth 4 file I showed that this :w2:

lived, and did not look for another :w2:

to live. That would have been overkill.

One advantage of iterative deepening, or at least, reading to a certain depth, is that you achieve thoroughness systematically, not haphazardly.

As most of my readers know, I am not a fan of the advice, for amateurs, anyway, not to look at the answers. Even Cho U, a modern master of tsumego, has revealed that as a kid he looked at the answers.

Instead I have advised people to set aside a certain length of time, 30 seconds, one minute, two minutes, 15 minutes, whatever, to solve a problem, and then look at the answer. OC, that's just the first time around. It is necessary to overlearn the solution. Now I wonder if it is better to set a certain depth to read, and then stop. This is a depth 5 problem. You won't solve it at depth 4. But you could start off reading systematically at depth 4, at which point the rest is obvious.

This problem has illustrated the importance of good heuristics. Let me add other learning, as well.

Click Here To Show Diagram Code: [go]$$Bc Chunking $$ -------------- $$ | . . . . . . . $$ | X X X X . . . $$ | 3 O O 2 X . . $$ | . 4 1 O X . . $$ | O O O X X . . $$ | . O X . . . . $$ | O O X . . . . $$ | . X X . . . . $$ | . . . . . . . $$ | . . . , . . .[/go]

For me, the sequence, :w2:

-

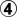
is a chunk that makes an eye. I therefore do not need to look at other options for :b3:

. The chunk is indivisible.

Click Here To Show Diagram Code: [go]$$Bc White lives, depth 2 $$ -------------- $$ | . . . . . . . $$ | X X X X . . . $$ | C O O 1 X . . $$ | C C 2 O X . . $$ | O O O X X . . $$ | . O X . . . . $$ | O O X . . . . $$ | . X X . . . . $$ | . . . . . . . $$ | . . . , . . .[/go]

It is also obvious to me that :w2:

makes a second eye. Now, it takes two more moves for that eye to be closed, but, as we say, the three :ec:

points, along with the adjacent White stones, form an eye space with the value of one eye for White. Informally, White has an eye. Now, that is something that maybe most 5 kyus do not know, but experienced tsumego solvers know that White can make an eye in that space, even if Black goes first. By simple arithmetic Black's play takes away one point and so does White's reply, but that leaves one open point for the eye.

OC, I did not rely upon such knowledge in illustrating iterative deepening, but in actuality it is quite useful.

Tryss · **#760**

All in all, I don't see how iterative deepening help in these kind of situations compared to a Depth-first search with backtracking.

To truly solve a problem like this, you need to fully explore all the branch of the tree, it doesn't matter in what order.

This 'n' that

Who is online